|
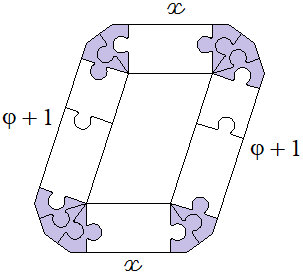
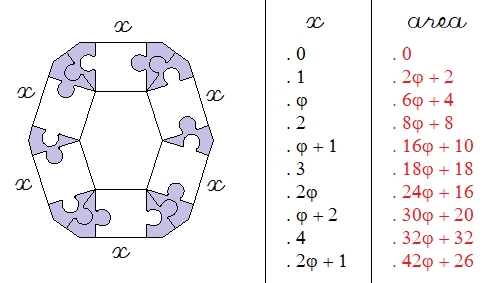
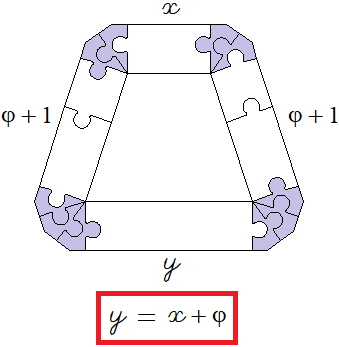
Challenges La Ora Stelo 1 • Diamonds. • Trisoceles Trapezoids. • 2phi. • 2nd type trisoceles Trapezoids. • Barrel Hexagons. • Robin King's trapezoids. • Robin King's parallelograms. |
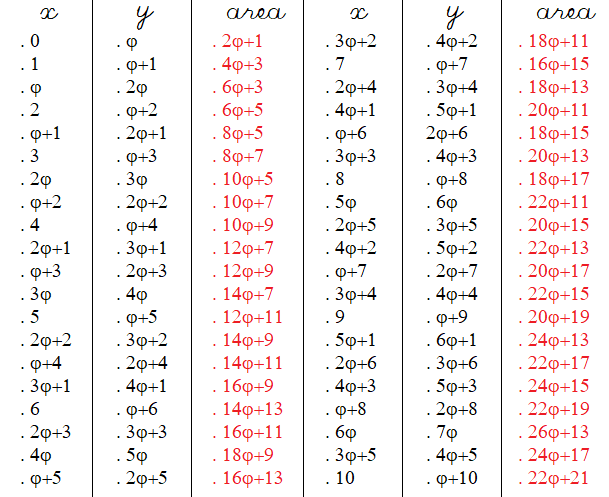
At the end of this series, for I dedicate this series to Robin King who found solutions to the first 39 trapezoids of this series ; she did not find a solution to the 40th ; neither do I and I don't know if there is a solution.. This series is copied from the previous series with sides of length
φ + 1 but the trapezoids are replaced by parallelograms.![]()
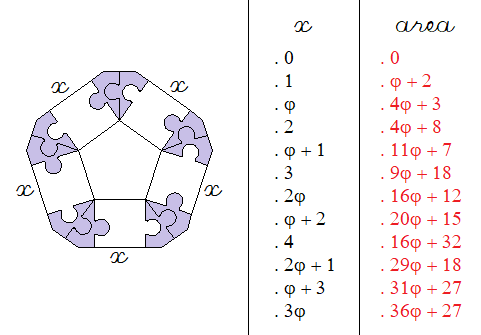
![]()
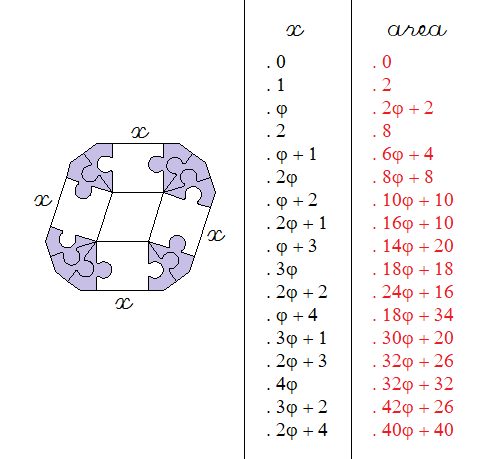
![]()
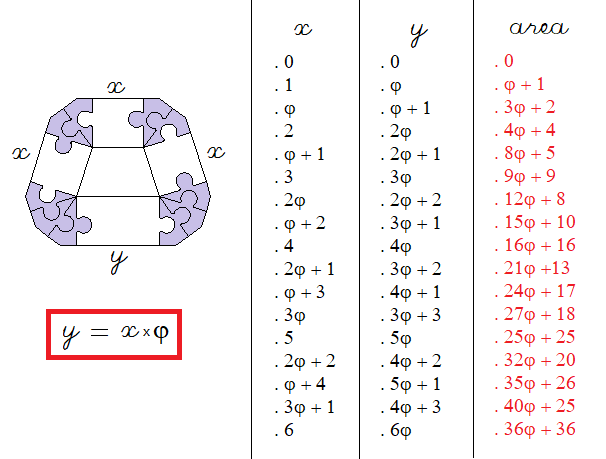
![]()
These are in fact 3 series based on the 3 polyores of area
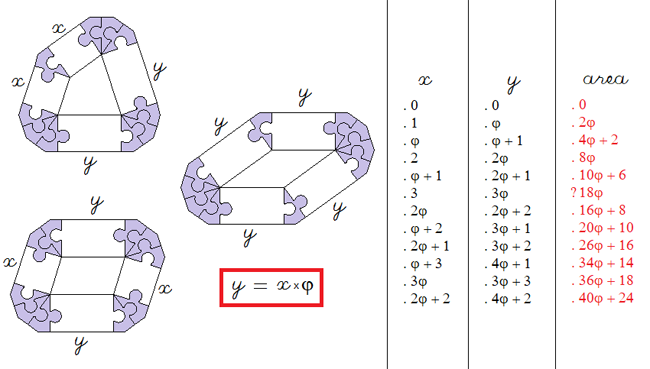
![]()
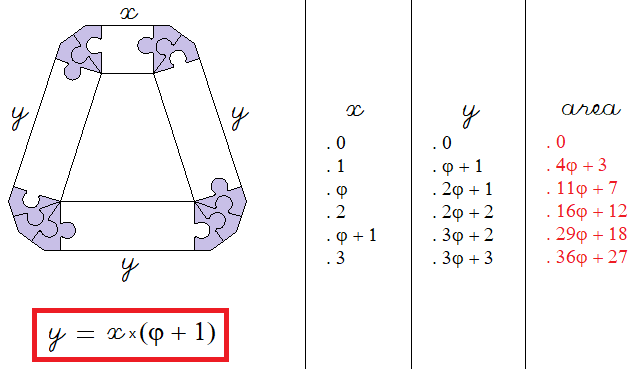
![]() = 3, we have an area of 36φ + 27 ; in the series of regular pentagons, for
= 3, we have an area of 36φ + 27 ; in the series of regular pentagons, for ![]() = 3φ, we also have an area of 36φ + 27.
= 3φ, we also have an area of 36φ + 27.
Is it possible to find a set of polyores whose total area is 36φ + 27 and which covers both the trapezoid and the pentagon ?![]()
![]()
I called it "Series of Robin King's parallelograms" because I think she would have liked this challenge. If someone gives me the solutions of the 40 parallelograms, then I would extend the list.